Recent Advances in Physical Reservoir Computing: A review
Study on the applications of neuromorphic computing
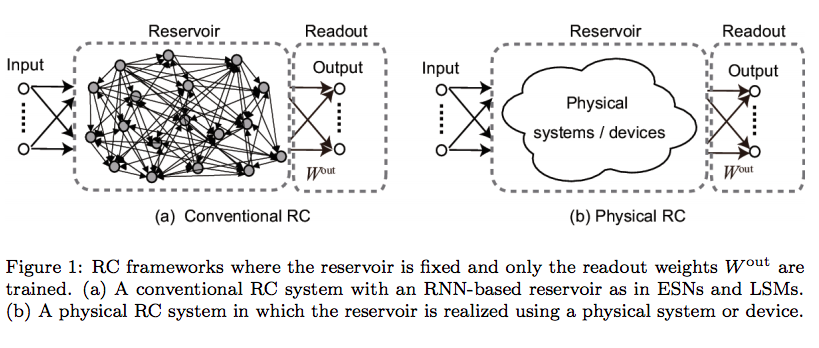
- A reservoir computing system consists of a reservoir for mapping inputs into a high-dimensional space and a readout for extracting features of the inputs. Further, training is carried out only in the readout.
- Another advantage is that the reservoir can be realized using physical systems, substrates, and devices, instead of recurrent neural networks.
- Our objective is to provide a comprehensive viewpoint with regard to interdisciplinary studies on physical RC by classifying them according to the type of the physical phenomenon in the reservoir. Toward this end, we summarize the characteristics of individual physical reservoirs. Our classification, which highlights the similarities and differences among different physical reservoirs, is useful for gaining insights into the further developments of physical RC.
- In the early 2000s, ESNs (Jaeger, 2001a; Jaeger and Haas, 2004) and LSMs (Maass et al., 2002; Maass, 2011) were independently proposed as seminal RC models.

Echo state machine
- The ESN was proposed by Jaeger (Jaeger, 2001a; Jaeger and Haas, 2004).
- The performance of the ESN depends on the design of the RNN-based reservoir. To approximate the input signal, the RNN-based reservoir should have the echo state property, whereby it asymptotically eliminates any information from the initial conditions (Jaeger, 2001a).
Liquid state machine
- The purpose of LSMs is to develop biologically relevant learning models using spiking neural networks with recurrent architectures (Fig. 1(a)). The spiking neurons are excitatory or inhibitory. Although they are principally modeled with integrate-and-fire neurons, other biologically plausible models can also be used
- The topology and connectivity of the RNN in the LSM follow the constraints of biological neural networks. Specifically, the probability that two neurons are connected depends on the distance between their positions. Such a reservoir is often called a liquid and the LSM operation is called liquid computing because it is similar to excitable media exhibiting ripples in response to external stimulation inputs.
Recent trend of RC
 Requirements for physical reservoir
Requirements for physical reservoir
- high dimensionality
- nonlinearity
- fading memory (short-term memory) - to ensure that the reservoir state is dependent on recent-past inputs but independent of distant-past inputs.(echo state property)
- seperation property - distict signals into different classes - insensitive to unessential small fluctuations (noise)
Dynamical systems models for RC
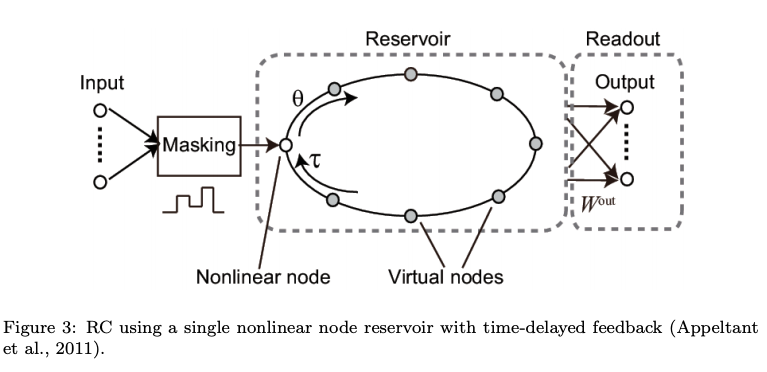
- Delayed dynamical systems
- The reservoirs in ESNs and LSMs generate high-dimensional signals using a network of interacting neuron nodes, which are regarded as a special class of high-dimensional dynamical systems. Another way to generate high-dimensional patterns is to use a time-delayed dynamical system
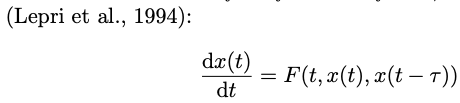
- The reservoirs in ESNs and LSMs generate high-dimensional signals using a network of interacting neuron nodes, which are regarded as a special class of high-dimensional dynamical systems. Another way to generate high-dimensional patterns is to use a time-delayed dynamical system
Ref. Reservoir Computing with an Ensemble of Time-Delay Reservoirs
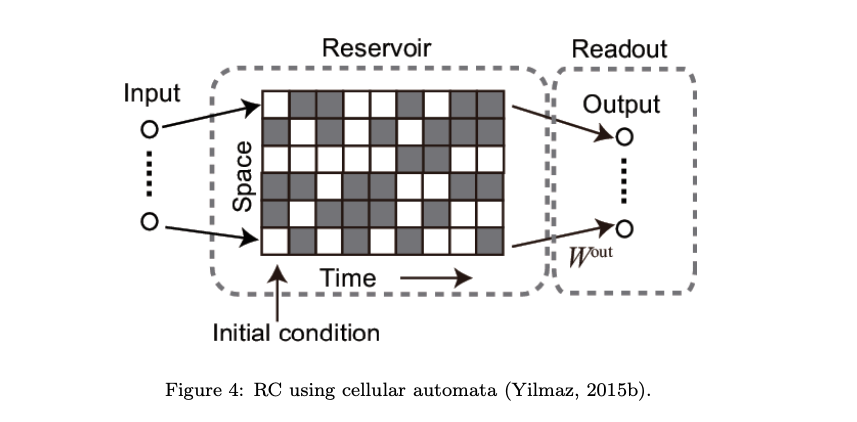
- Cellular automata
- A cellular automaton (CA) is a simple dynamical system model where both state and time are discrete (Wolfram, 2018). The discrete states on the cells are updated according to a given (local) evolution rule. Depending on the rule, the CA can exhibit rich behavior, including ordered, critical (or the edge of chaos), and chaotic dynamics, in spite of its simplicity. It is heuristically conjectured that the computational capability of CA is maximized at the edge of chaos.
- This conjecture has been confirmed in a numerical study on RC based on a random Boolean network, which is an extended version of CA (Snyder et al., 2013). Other studies employed CA-based reservoirs as shown in Fig. 4 (Yilmaz, 2014, 2015a,b).
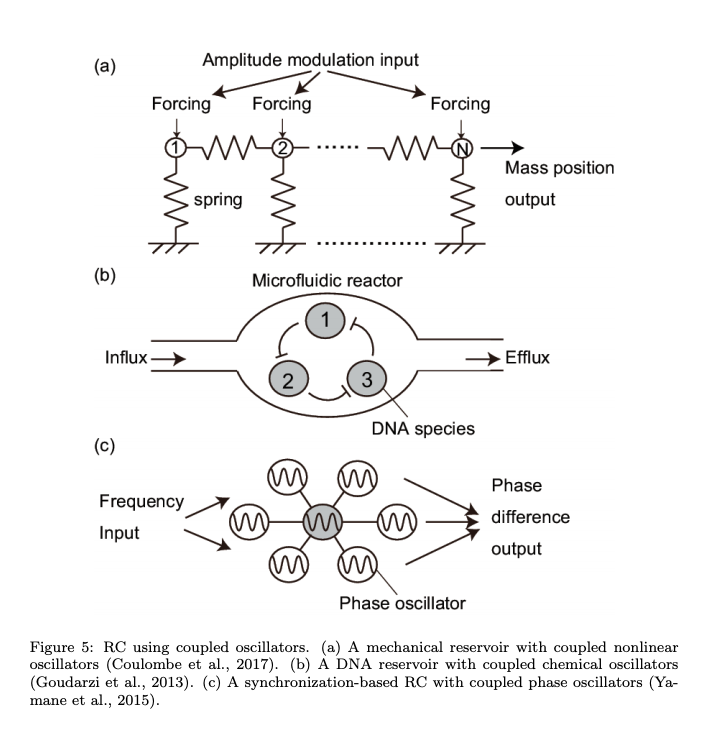
- Coupled oscillators
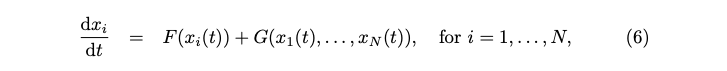
- Electronic RC
- …
- Time-delay circuits
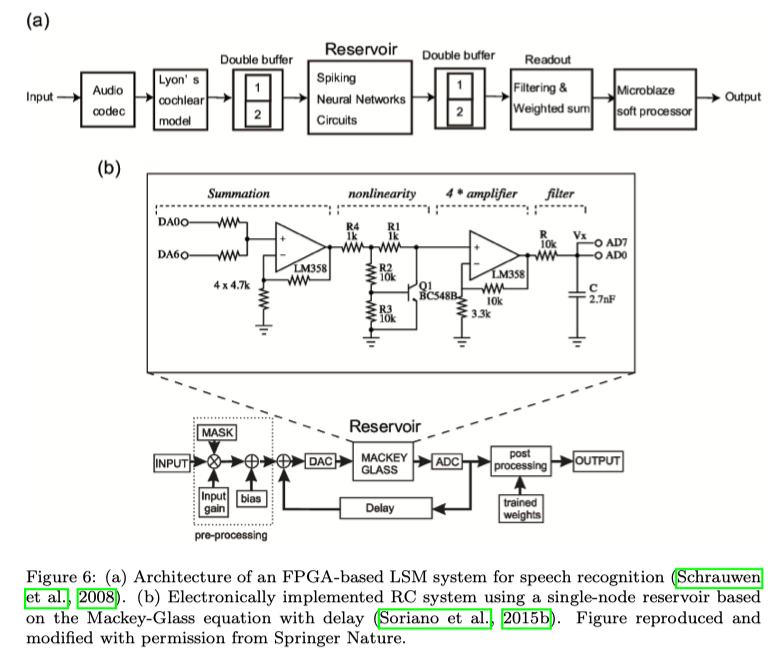
- A simpler architecture is a single-node reservoir with delayed feedback, as described in Sec. 3.1. A single-node reservoir imposes less hardware requirements compared to a network-type reservoir consisting of a large number of units (Soriano et al., 2015a). An electronic implementation of a single-node reservoir with a delay line was demonstrated using analog circuits as shown in Fig. 6(b) (Soriano et al., 2015b). The effect of the quantization noise generated by AD and DA conversion of the signals on the computational performance was investigated. A digital FPGA implementation of a single-node reservoir with delayed feedback was adopted for wave classification and time series prediction (Alomar et al., 2015). In (Haynes et al., 2015), a single autonomous Boolean node reservoir was implemented on an FPGA and employed to reproduce a three-input XOR gate. In other studies, a single spike-based node with delayed feedback was implemented with analog circuits (Zhao et al., 2016; Li et al., 2017).
- Analog circuit (Soriano et. al. 2015)
- FPGA (Alomar et. al. 2015) - Memristive RC
Memristive RC
- Classification of memristive RC
- neuromemristive reservoirs consisting of both neuron circuits and memristor synapses
- memristor-based reservoirs without neuron elements